A New Horizon in Football Forecasting: The Betting Odds-Based ELO System
A novel forecasting model that integrates betting odds information into the established ELO rating system, outperforming the traditional model.
Introduction
The introduction of this research paper delves into the multifaceted nature of sports event forecasting, particularly in the context of football matches. It highlights the significant interest from both the scientific community and the economic sphere, especially within the expansive betting market. The study positions football as an ideal domain for developing and evaluating forecasting methodologies due to its regular occurrence, high public engagement, and ample availability of data.
Identifying accurate sports forecasting methods is crucial, not only for economic gains but also for gaining a deeper understanding of the underlying processes. The paper outlines three primary challenges in sports forecasting: investigating team or player quality using comprehensive datasets and fitting appropriate mathematical models (referred to as the rating process), deriving forecasts through statistical methodologies (the forecasting process), and rigorously testing the forecasted outcomes against real data.
The text further delineates four major sources of forecasts studied in this context:
Human judgement involves seeking predictions from individuals with varying degrees of expertise in sports-related forecasting tasks.
Rankings utilize official rankings, such as the FIFA World Ranking in football or the ATP ranking in tennis, to derive forecasts for future matches and tournaments.
Mathematical models involve the use of existing or novel mathematical and statistical approaches to forecast sports event outcomes.
Betting odds, provided by bookmakers and betting exchanges, are utilized as forecasts for underlying sports events.
The paper sets the stage for investigating and comparing these diverse sources of forecasts, acknowledging the challenges and complexity inherent in sports forecasting while emphasizing the importance of developing accurate and reliable methodologies in this domain.
Human judgement
The section explores the assessment of human judgement in forecasting football events. Various studies have analyzed the predictive quality of human forecasts in this domain. Notably, these investigations have revealed that individuals commonly regarded as “football experts” do not consistently outperform laypeople when it comes to simple football-related forecasting tasks. Surprisingly, in certain cases, laypeople have performed better than experts. For instance, research has indicated that a straightforward model relying on the FIFA World Ranking can outperform expert forecasts in predicting football match outcomes.
Even more intriguingly, expert forecasts provided by tipsters in sports publications have been shown to be less accurate than a basic approach of consistently choosing the home team to win. However, there’s a nuanced finding suggesting that in more intricate forecasting tasks, such as predicting exact scores or match statistics, experts tend to perform better than laypeople. This contrast in performance highlights the complexity of forecasting tasks and the varying degrees of expertise across different types of predictions within football events.
Rankings
The section delves into the efficacy of rankings in forecasting sports events, highlighting their limitations and utility. Rankings, primarily designed to reward past successes rather than predict future performance, often lack complexity and depth required for accurate predictive purposes. They’re typically simplistic and may not incorporate nuanced information essential for making precise future performance estimates for teams or players. Although they serve as straightforward tools for fairness and comprehension, their predictive accuracy is questioned in forecasting.
Research indicates that while rankings have been deemed useful predictors in sports like football, tennis, and basketball, they often fall short compared to other forecasting methods. Betting odds and mathematical models have demonstrated superior predictive capabilities, outperforming rankings in forecasting tasks. Despite their simplicity and widespread use, rankings may not possess the depth or sophistication needed to accurately predict future outcomes in sports events when compared to more complex predictive methods like mathematical models and betting odds.
Mathematical models
The section discusses the utilization of mathematical models, particularly focusing on the ELO rating system, renowned for ranking and rating sports teams or players. Originating in chess, the ELO system has been widely adopted and applied to various sports like football, tennis, and Australian rules football. One notable extension of the ELO system is by Hvattum and Arntzen, who incorporated logit regression models to calculate probabilities for three match outcomes (Home/Draw/Away) based on the ELO ratings. Their study showcased that this ELO-based approach outperformed models relying on an ordered probit regression method introduced by Goddard. However, despite its effectiveness, the ELO approach was found to be inferior to betting odds in predictive accuracy.
Betting odds
The section begins by examining betting odds as a forecasting source, differentiating it from traditional expert opinions by emphasizing the financial consequences faced by bookmakers for inaccurate odds. Despite this, betting odds have shown exceptional predictive quality, often outperforming expert opinions and various quantitative models. Studies indicate that betting odds generally excel in forecasting football outcomes, surpassing other methodologies, such as the ELO rating or FIFA World Ranking, in accuracy for major tournaments like the European Championship 2008.
While acknowledging the predictive strength of betting odds, empirical evidence indicates their imperfections, including the favorite-longshot bias and instances where model-based approaches yield positive betting returns. Notably, betting odds are considered a benchmark for testing the predictive efficacy of mathematical models. However, existing studies predominantly focus on comparing different forecasting sources or approaches rather than integrating the potential of both betting odds and mathematical models to innovate new forecasting techniques.
The text highlights the limited exploration of using existing forecasts, such as betting odds, to derive team qualities and contribute to performance analysis. A study attempted an “inverse” simulation using betting odds from the European Championship 2008 to obtain team ratings, shedding light on differences between team quality and probability of winning due to tournament draws. However, studies seldom consider using betting odds from single matches to establish team ratings or forecast future matches based on prior odds.
This study introduces a new model aiming to blend the strengths of mathematical approaches with the information richness of betting odds. Unlike models improving upon betting odds, this model focuses on investigating the transferability of prior forecasts to future predictions, constructing enhanced ratings, and gaining practical insights into performance analysis. It explores the worth of betting odds known before a match compared to results known afterward. The resulting rating, derived from prior forecasts, reverses the forecasting process, deducing team quality from historical forecasts. This rating framework enhances traditional methods and effectively extracts information from betting odds for practical football team quality analysis. Additionally, the study demonstrates the model’s applicability in analyzing individual team quality development over time, assessing the league tables’ explanatory power, and addressing rating models’ theoretical limitations concerning the network structure of matches.
Method
Data
The methodological approach adopted in this research involved collecting extensive football match data covering 10 seasons from prominent European leagues: the English Premier League, the German Bundesliga, the Spanish Primera Division, and the Italian Serie A. This data, comprising nearly 14,500 domestic matches, was obtained from http://www.football-data.co.uk. Additionally, data for 10 seasons from major international club competitions (UEFA Champions League and UEFA Europe League) involving teams from the mentioned leagues were gathered from http://www.oddsportal.com, totaling more than 450 international matches and creating a database of approximately 15,000 matches.
The core data set for each match encompassed various attributes such as match date, home team, away team, home goals (full time), away goals (full time), and betting odds for home win, draw, and away win. To ensure a comprehensive reflection of the betting market rather than being bookmaker-specific, the analysis employed average betting odds derived from multiple bookmakers. The average betting odds were calculated based on data from five or more bookmakers for international matches and 20 or more bookmakers for domestic matches. However, specific matches, namely Cagliari vs. Roma (23.09.12) and Sassuolo vs. Pescara (28.08.16), were omitted from the dataset due to decisions made by the federation affecting the match outcomes. Moreover, the final matches from the Champions League and Europe League, which are played at neutral locations, were entirely excluded from the dataset. Detailed information on the number of matches for each season and competition can be found in Table 1 of the research.
Transferring betting odds to probabilities
The process of converting betting odds into probabilities serves as a fundamental technique in deriving forecasts for sports events, owing to the demonstrated effectiveness of betting odds in various studies. In this study, to transform betting odds into probabilities, a straightforward method was applied. When the betting odds contain no bookmaker margin, the inverse of the betting odds for each possible outcome of a match represents its respective probability of occurring.
To eliminate the bookmaker margin from the odds and ensure that the derived probabilities sum up to 100%, the widely used method of basic normalization was employed. This technique effectively removes the overall bookmaker margin. However, it’s important to note that this method assumes a proportional distribution of the bookmaker margin across all potential outcomes of a match (such as home win and draw), which might be considered a simplification.
Despite potential criticisms of the basic normalization approach due to its simplifying assumptions regarding the distribution of the bookmaker margin, the relatively small margins present in the dataset used in this study (with an average bookmaker overround of 1.064, corresponding to a theoretical payout of 94.0%) support the acceptance of this simplification. More details regarding the margins are provided in Table 1 and the supplementary information file accompanying the study.
Rating systems
The ELO rating system, initially developed for chess, has been extensively applied to rate football teams, demonstrating its adaptability and effectiveness in various sports domains. This model operates on the principle of computing an anticipated outcome for each match based on the current ratings of the involved teams. Subsequently, once the match concludes, the actual result is known, and adjustments are made to the ratings of both participating teams. Larger discrepancies between the actual and expected outcomes prompt more significant adjustments to the ratings, thereby ensuring the ratings dynamically evolve over time with each new match result. This dynamic nature allows for continual updates and refinements of team ratings based on their performance in subsequent matches.
ELO-Result
The ELO-Result model calculates the expected outcome of a match between two teams based on their respective ELO ratings, denoted as Hi and Ai for the home and away teams, respectively. This model incorporates a parameter ω to represent the home advantage in ELO points, alongside parameters c and d, which influence the rating’s scale. Typically, the values chosen for these parameters are c = 10 and d = 400, as employed within this study.
Post-match, the actual outcome (aH) for the home team is observed, wherein aH = 1 denotes a home team win, aH = 0.5 signifies a draw, and aH = 0 represents a loss for the home team. The actual outcome for the away team (aA) is derived as aA = 1 − aH. Subsequently, both team ratings are adjusted based on the observed outcome, utilizing an adjustment factor denoted as ‘k’, a variable to be determined through calibration. This ELO-Result model stands as a classic approach in ELO rating systems, having roots in both chess and football domains. For further detailed insights into the classic ELO rating methodology applied in these contexts, references such as [26], [13], and [3] offer comprehensive information.
ELO-Goals
The ELO-Goals model is an adaptation of the traditional ELO rating system that integrates the absolute goal difference (δ) observed in a match into its calculations. This modification adjusts the parameter ‘k’ within the ELO model, modifying it to incorporate the goal difference, indicating a broader utilization of match-specific data beyond solely match outcomes.
The formula for ‘k’ in the ELO-Goals model has been adjusted to account for the goal difference, providing a more nuanced representation of team performance in a match. This adaptation extends the traditional ELO model by considering the goals scored, thereby offering a more detailed assessment of team performance compared to the standard ELO model that relies solely on match results. This modified calculation methodology is drawn from a study, leading to the introduction of the ELO-Goals model. It’s worth noting that the World Football Elo Ratings, a widely recognized reference in football ratings, also incorporates goals in its calculations, albeit using a slightly different methodology.
ELO-Odds
The ELO-Odds model is a novel approach that integrates betting odds into the ELO rating methodology for football match forecasting. Unlike conventional ELO-based models that use observed match results, the ELO-Odds model leverages probabilities derived from betting odds as substitutes for actual match outcomes in its calculations.
Similar to the ELO-Result model, the ELO-Odds model computes expected match results based on current ratings of participating teams. However, instead of employing the actual match result, the model incorporates probabilities for home win (pH), draw (pD), and away win (pA) derived from betting odds as substitutes for observed match outcomes. This innovative approach aims to capture additional information by indirectly deriving it from betting odds, thereby broadening the scope beyond traditional match results or goal differentials.
A distinctive feature of the ELO-Odds model is its exclusive reliance on pre-match information obtained from betting odds, disregarding any post-match match results or information. By using betting odds before the match as a proxy for actual outcomes, this model focuses solely on pre-match data, neglecting observed results following the match. This restrictive aspect underscores the model’s reliance on pre-match information exclusively gleaned from betting odds, representing an innovative yet limited method in football match forecasting methodologies.
Statistical framework
The statistical framework employed in this study draws from established methodologies outlined by Hvattum and Arntzen. Adopting their approach, the ELO models used in this research follow a specific sequence:
Initially, across a ten-season period (07/08–16/17), ELO ratings for each football team are computed and continually adjusted after every match. A home advantage factor of ω = 80 is utilized, while teams commence with an initial rating of 1,000 points before their first match in the initial season. Notably, promoted teams in subsequent seasons inherit the ratings of relegated teams from the prior season, ensuring a consistent sum of ratings across the participating teams in the leagues. This approach is beneficial as it considers the relative weakness of promoted teams, utilizing the relegated teams’ ratings as more informative estimators of team quality.
The initial two seasons (07/08 & 08/09) are used solely to establish initial ratings for each team. Subsequently, over the following three seasons (09/10–11/12), the rating differences between the home and away teams are calculated for each match. These rating differences serve as the sole covariate in an ordered logit regression model. The resulting logistic functions from this regression model transform these rating differences into probabilities for home wins, draws, and away wins. In the last five seasons (12/13–16/17), these calculated probabilities are used as match forecasts.
Finally, the predictive quality of the forecasts is assessed using the informational loss (Li) as a measure, wherein minimizing this loss is akin to maximizing the likelihood function. The study conducts paired t-tests to ascertain the significance of differences in the loss functions between two models. Figure 1 illustrates a visual representation of the rating process, forecasting process, and testing process employed in the study, delineating the flow of these methodologies. This meticulous process ensures a rigorous evaluation of predictive quality while leveraging established statistical frameworks.

Results
Parameter calibration
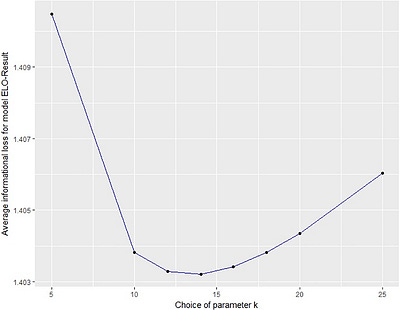
The results section of this study focuses on the parameter calibration required for the three models: ELO-Result, ELO-Goals, and ELO-Odds. These models necessitate calibration of specific parameters: ELO-Result and ELO-Odds require a single parameter, denoted as k, while ELO-Goals requires two parameters, k0 and λ.
The examination involved assessing the informational loss across various parameter values for each model, as showcased in Table 2 and visualized in Figures 2, 3, and 4. The analysis determined the optimal parameters for each model: k = 14 for ELO-Result, k0 = 4 and λ = 1.6 for ELO-Goals, and k = 175 for ELO-Odds.

A notable observation is the substantial difference in the adjustment factor k between ELO-Result and ELO-Odds. This variance can be explained by two factors. Firstly, the actual results in ELO-Result (0, 0.5, or 1) naturally deviate more from the expected results than in ELO-Odds, hence requiring a smaller adjustment factor. Secondly, the outcomes in ELO-Result are more influenced by randomness, leading to the necessity of a lower adjustment factor to prevent excessive adaptation to recent results.
Although the study selected parameters based on the best results obtained, there’s a caution against overfitting the data. Yet, it’s evident that the outcomes are not highly sensitive to the parameter choice, particularly when compared to the sensitivity to model choice, as elaborated in the subsequent section. This signifies a robustness in the results obtained with respect to variations in the chosen parameters.
Predictive quality
The analysis of predictive quality revealed crucial insights into the performance of various forecasting methods. Betting odds emerged as the top-performing method, showcasing superior predictive quality compared to ELO-Odds, which itself outperformed ELO-Goals significantly. These findings aligned with earlier research by Hvattum and Arntzen conducted on different data, encompassing four European leagues and two international competitions.

The superiority of ELO-Goals over ELO-Result emphasized that the goal difference in a match contains more pertinent information regarding a team’s quality than the simple match result. This corroborated findings from previous studies, which demonstrated that average goal differences serve as a more accurate measure of team quality compared to average points earned over a set of matches.

However, the most striking and novel revelation was the superiority of ELO-Odds over ELO-Goals, underscoring the significance of forecasts derived from past matches as a valuable source for rating teams. Notably, this result retained its significance across various parameter choices, showcasing the robustness of the finding. Essentially, this indicates that betting odds known before a match possess more informative insights into team quality than the results observed post-match. This divergence might stem from the notion that match results represent a realization of the underlying probability distribution, while betting odds encapsulate this distribution.
Despite the success of ELO-Odds in utilizing betting odds as a foundation for forecasts, it falls short in extracting all available information. It solely aggregates team-specific details from the odds, overlooking factors such as motivational aspects, team injuries, or changes in line-ups between matches, which betting odds might encapsulate. Furthermore, the model’s reliance on an ordered logit regression with the ELO difference as the sole covariate might be a limiting factor, highlighting that an accurate rating does not always guarantee an accurate forecast.
Analyzing individual team ratings
The paper delves into analyzing individual team ratings using the ELO-Result and ELO-Odds models, particularly emphasizing their effectiveness in estimating team quality based on football matches. One crucial aspect involves verifying the comparability of these ELO measures to evaluate team quality estimation. Due to the construction of the ELO calculation where points gained by one team are equally lost by another, the ratings across different models are comparable in size, allowing for detailed analysis and insights into team quality and performance.
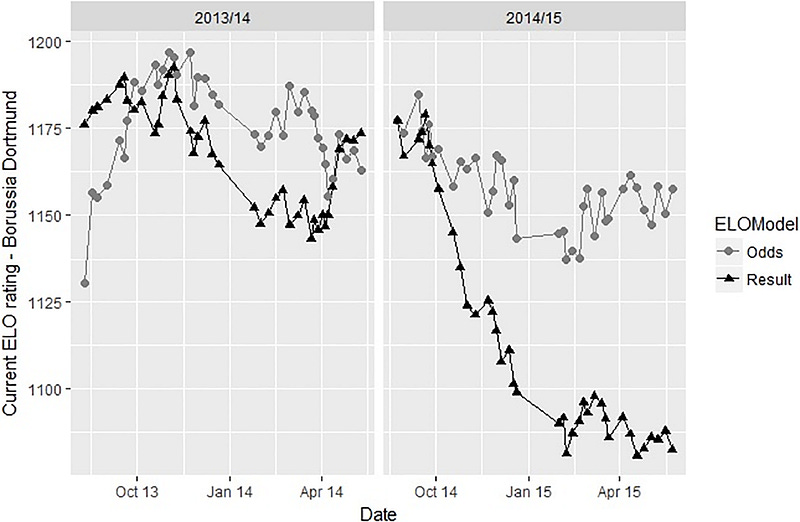
Illustrative examples featuring Borussia Dortmund and Leicester City highlight the divergence between ELO-Result and ELO-Odds ratings, offering valuable insights into team quality estimation. For Borussia Dortmund, both models aligned closely, showcasing negligible differences until a period of prolonged unsuccessful results significantly affected their ratings in ELO-Result, whereas ELO-Odds showed only a minimal reaction, indicating a weaker modification of the team’s perceived quality. Subsequent successful performances aligned more with the ELO-Odds judgment.
Conversely, for Leicester City, a substantial gap emerged between ELO-Result and ELO-Odds ratings throughout the 2014/2015 season. The market judgment, reflected by ELO-Odds, rated Leicester City higher than their actual results. Their remarkable triumph in the 2015/2016 season, winning the Premier League, saw a substantial increase in ELO-Result but a more muted rise in ELO-Odds, suggesting the market’s cautious assessment. Leicester’s subsequent 12th-place finish further aligned with the market’s prudent judgment rather than the ELO-Result-based rating.
These case studies underscore the effective use of a betting odds-based rating system for practical insights into football team quality. They notably highlight that football match results might inadequately capture team quality due to the inherent randomness in goal-scoring, consistent with prior research highlighting the unpredictability of scoring goals in football. This accentuates the potential for advanced performance indicators using positional match data to provide a more comprehensive evaluation of team quality.
However, it’s crucial to acknowledge the uniqueness of these situations and the underlying complexity of various factors influencing team performance, such as coaching changes, psychological impacts, or unexpected events that might not be captured solely through match results.
Analyzing league tables
The paper conducts an analysis comparing the final league table of the 2013/2014 season in the Spanish Primera Division with rankings based on average ELO-Odds ratings throughout the season. This comparison sheds light on the differences between teams’ standings based on their performance results versus their market valuations derived from betting odds.
The league table generally aligns closely with the market valuations, reflecting similarities between the two rankings. However, several noteworthy discrepancies stand out. Despite Atletico Madrid winning the title, the betting market ranked them third behind FC Barcelona and Real Madrid. While this might align with the expectation given the historical dominance of Barcelona and Real Madrid, it showcases a difference between market valuation and actual outcome. The differences are more intriguing for less successful teams. Levante UD, according to the market, was deemed the worst team during the season, yet they finished a commendable 10th in the league. Conversely, Betis Sevilla, despite being ranked 11th by the market, was relegated at the end of the season.
This comparison highlights the divergence between teams’ perceived quality based on market valuation and their actual performance results. It emphasizes the potential limitations of focusing solely on match outcomes in evaluating team performance. While the exact mechanisms of performance analysis within professional football clubs remain opaque, the study suggests that comprehensive performance analysis, considering various information sources beyond just match results, could be pivotal. It implies that club officials should consider a broader range of data and insights to evaluate the work of players and coaches effectively.
Betting returns
The paper delves into the assessment of a quantitative model for predicting football match outcomes, highlighting the common practice of evaluating these models through the lens of financial returns from betting strategies. However, it draws a crucial distinction between the profitability of betting strategies and the accuracy of predictive models based on statistical measures.
While the study calculated betting returns for different ELO models, it emphasizes that achieving positive betting returns doesn’t inherently signify superior predictive quality in the model. It uses the example of a simplistic model assigning 100% winning probability to each away team. Despite yielding positive betting returns, this approach wouldn’t be considered a reliable probabilistic forecasting model. This illustration underscores the difference between finding profitable betting strategies and identifying accurate predictive models.
Specifically, the ELO-Odds model aims to amalgamate the strengths of betting odds and mathematical models by leveraging betting odds’ information within mathematical frameworks. As a result, it is inherently designed to extract information from betting odds rather than to consistently generate positive betting returns. Therefore, the study’s primary focus lies in evaluating the predictive quality of forecasting models using statistical measures and their efficacy in providing insights for performance analysis rather than solely assessing financial profitability.
Discussion
The discussion within the paper delves into several key aspects of the study’s methodology, findings, and future directions. One major emphasis is the innovative approach of using betting odds as a source of information rather than aiming to surpass or beat them. While betting odds are widely acknowledged for their predictive power, they haven’t been utilized as a foundation for creating rankings and ratings. The study successfully demonstrates the promise of extracting valuable information from betting odds, revealing the potential for insights that might otherwise be challenging to leverage in mathematical models.
Moreover, the paper underscores the transferability of results from prior studies concerning ELO-ratings in association football to a different dataset encompassing domestic and international matches. However, it cautions that the structure of the data heavily relies on the choice of teams and competitions, highlighting the complexity of data structures across different sports and contexts.
The study suggests that the ELO rating system might not be the optimal approach for certain data sets, particularly those characterized by indirect comparisons. It proposes leveraging the network structure of teams and matches for future rating approaches, anticipating more accurate estimations and a more streamlined initial rating derivation process.
Additionally, the discussion points out the complexities in evaluating rating and forecasting methods, attributing the quality of these models to their ability to estimate team ratings accurately and forecast outcomes based on those ratings. As the true quality of a team is never directly observable and subject to changes over time, the study acknowledges the challenges in proving the responsible factors for achieving predictive quality.
To enhance the understanding of rating model quality, the study recommends constructing theoretical datasets with known team qualities and simulated results, applying rating models to this data, and comparing calculated ratings with the known ones — a strategy to evaluate the models under controlled conditions.
Furthermore, the study highlights the importance of expert judgement and crowd wisdom in quantitative sports forecasting models. It cites examples of successful integration of collective judgements from websites and attempts to extract crowd wisdom from social media data, showcasing their potential for refining sports forecasting models.
Conclusion
In this study, the utilization of betting odds as a crucial tool for information processing and sports event forecasting is highlighted. Betting odds serve as an indicator of anticipated success in upcoming matches, allowing the direct translation of market expectations into a quantitative team rating — an estimation of team quality. Notably, this rating model based on betting odds demonstrates superiority over traditional metrics like match results or goals, especially within the framework of an ELO forecasting model.
The study acknowledges the need for future research to delve into match-related aspects, such as motivational factors or line-up changes, which might influence betting odds but are not necessarily linked to overall team quality. The emphasis is placed on the potential of rating methods and forecasting models to unravel underlying processes in sports, emphasizing the strong connection between forecasts and performance analysis.
A crucial point established in this research is that relying solely on results and goals as sources of information for rating football teams and predicting match outcomes is insufficient. It underscores the significant value of expert opinions in enhancing forecasting models and suggests the inclusion of crowd wisdom sources into mathematical approaches. The study anticipates the evolving potential of using vast social media datasets (like Twitter data) or search engine data (such as Google search queries) in rating and forecasting sports events.
Addressing the limitations in current sport-scientific studies that often rely on win/loss records, goal tallies, or league positions as measures of team strength, the paper advocates for the incorporation of a measure based on betting odds. This betting odds-based approach, exemplified by the ELO-Odds rating in this study, is deemed more suitable than traditional measures, offering a more nuanced and improved method to evaluate team qualities. This, the study suggests, could pave the way for future research to leverage the ELO-Odds rating as an enhanced approach in assessing and understanding team strengths.
References
Wunderlich, F., & Memmert, D. (2018). The betting odds rating system: Using soccer forecasts to forecast soccer. PloS one, 13(6), e0198668. https://doi.org/10.1371/journal.pone.0198668