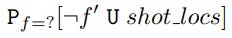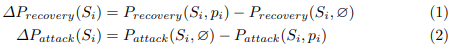Analyzing Defensive Strategies in Professional Football Using Markov Models
A Markov Decision rocess (MDP) approach combined with probabilistic model checking to analyze defensive strategies in soccer.
The article “Reasoning about Goal-Directed Policies in Professional Soccer using Probabilistic Model Checking” by Maaike Van Roy, Wen-Chi Yang, Luc De Raedt, and Jesse Davis presents a novel Markov decision process (MDP) for modeling the behavior of a soccer team that possesses the ball. The authors employ techniques from probabilistic model checking to analyze the MDP and reason about the goal-directed policies that soccer players follow, specifically in the context of defense. The objective of this article is to gain insight into various ways an opponent may generate dangerous situations where they can score a goal, and to assess how much a team can lower its chance of conceding by employing different ways to prevent these situations from arising. The authors provide multiple illustrative use cases by analyzing real-world event stream data from professional soccer matches in the English Premier League.
In this review article, we will provide an in-depth analysis of the paper and discuss its contributions, limitations, and implications for future research. We will begin by providing an overview of the paper and its motivation, followed by a detailed discussion of the proposed MDP model and probabilistic model checking techniques used for analysis. We will then examine the results of the analysis, including the defensive strategies employed by teams and their effectiveness in reducing the chance of conceding a goal. Finally, we will conclude by summarizing the key contributions of the paper and identifying areas for future research.
Introduction
The paper discusses the application of Markov models in the context of professional sports matches, specifically in soccer, to understand opponent behavior and to aid coaches in their tactical planning. The objective is to reason about the goal-directed policies that players follow to help teams minimize their chances of conceding a goal. The authors propose a two-step framework involving learning a team-specific Markov Decision Process (MDP) from event stream data and using probabilistic model checking techniques to reason about the learned policy. The MDP’s state space consists of locations on the pitch, and actions involve moving between these states or shooting on goal. The probabilistic model checker PRISM is used to reason about the MDP in different ways, such as understanding how an opponent may generate a scoring opportunity, evaluating the effectiveness of defensive strategies, and estimating their effectiveness even if the opponent adapts to them. The paper provides a number of illustrative examples of tactical insights about teams in the English Premier League and contributes to the field by suggesting a real-world application of verifying properties of learned models in sports, proposing a novel MDP for modeling tactical behavior in soccer, and demonstrating how probabilistic model checking can aid coaches in their planning.
Preliminaries
In this section, the authors provide some background on Markov models and their applications to soccer, as well as an introduction to probabilistic model checking.
Markov Models
A Markov model is a probabilistic process that describes the transition between various states in a system. Specifically, a Markov Reward Process (MRP) is a Markov model that associates rewards or costs with each transition. An MRP is defined as a tuple (S, P, R, γ), where S is the set of states, P is the transition function, R is the reward function, and γ is a discount factor.
The authors also introduce the concept of a Markov Decision Process (MDP), which extends an MRP to allow transitions between states to depend on the action taken in a state. Additionally, a policy π can be defined for an MDP, which specifies the probability distribution over actions given a certain state. Together with the MDP, it defines the behavior of an agent.
Markov Models for Soccer
In this section, the authors discuss the use of Markov models in soccer, specifically for assigning a value to each on-the-ball action performed by players during a match. They note that Markov Reward Processes (MRPs) are typically used to model the in-game behavior of teams and divide a soccer match into possessions, where each possession is a sequence of consecutive on-the-ball actions carried out by the same team. Each action transitions the game from one state to another in the MRP, with the goal being to eventually reach a state where the team has a higher chance of scoring. Players continue to perform actions until one of two absorbing states is reached: a goal is scored and they receive a reward of 1 or the possession ends (e.g., a turnover occurs, a shot is taken and missed, etc.) and they receive a reward of 0. The value of a non-absorbing state is then the probability of eventually scoring from that state, which can be obtained using the standard dynamic programming approach. These values are then used to assign a value to all on-the-ball actions. The authors note that the probabilities in the model are learned from historical event stream data, which is collected by human annotators and includes attributes such as the type of action, start and end locations, timestamp, player who performed the action, and whether the action succeeded or failed. An example of a possession sequence for Manchester City is provided in Figure 1.

Probabilistic Model Checking
In this section of the paper, the authors introduce probabilistic model checking, which is a technique used to verify whether a probabilistic system satisfies a specific property. Probabilistic model checkers such as PRISM and STORM are commonly used to provide quantitative guarantees for systems with probabilistic behavior. The authors focus on reachability related properties in PRISM to reason about how an opponent reaches a dangerous situation. They use the probabilistic reachability property in PCTL∗ to evaluate whether a property holds in a state, which returns a true or false value. The authors specifically look at quantitative properties of the form P=?[α], which query the probability that α holds, returning a real number in the range [0,1]. In soccer, possession sequences can start anywhere on the field, and a property can be evaluated for any initial location or state. The authors use Pf=?[prop] to indicate that a property prop is evaluated for a state f, which returns the probability that prop holds in f.
MDP for Soccer
The authors propose a discrete soccer MDP for analyzing and verifying a team’s tactical or goal-directed behavior, which generalizes the existing MRP models for soccer. The proposed MDP has two actions: “shoot” and “move to”, allowing explicit reasoning about a team’s policy and tactical behavior in various situations. As stated before, the soccer MDP is defined as a tuple consisting of states (S), actions (A), transition probabilities (P), reward function (R), and a discount factor (γ). The set of states (S) consists of 89 field states and three absorbing states: loss of possession, failed shot, and successful shot. The partitioning of the field states is fine-grained where chances of scoring are higher and more coarse-grained where goal scoring chances are lower to ensure sufficient data in each state while being fine-grained enough to capture important differences between locations. The set of actions (A) includes moving to any field state and shooting. The transition probabilities (P) are defined for both the absorbing and field states. For the field states, the transition probabilities are defined for successfully moving to a new field state, losing possession, or scoring a goal. The reward function (R) is 1 only when a goal is scored and 0 otherwise. The long-term value of a state is given by the value function, which considers the policy to be followed and calculates the sum of the rewards discounted over time. The policy and transition model for a team can be learned from historical data by estimating all probabilities with simple counts. However, the chosen action space complicates this process, requiring the identification of intended end locations of failed movement actions. To solve this problem, the authors use a gradient boosted trees ensemble to predict the intended end location of actions based on several characteristics of the actions and what happened before those actions.
Reasoning about Soccer MDPs
This section of the research paper focuses on the application of the methodology mentioned earlier to learn team-specific policies and transition models of the underlying MDPs in the context of soccer. The authors use real-world event stream data from the 2017/18 and 2018/19 English Premier League (EPL) seasons, provided by StatsBomb, to create a team-specific MDP for each of the 17 teams that played in both seasons.
The team-specific policy, together with the MDP, is transformed into a MRP that probabilistic model checkers such as PRISM can analyze. By checking different properties against the MRP, the authors gain insight into how the team reacts to different situations. The objective of a soccer team is to score goals, which can be specified as a probabilistic reachability property. By checking this property against the team’s MRP, the authors produce a value function that assigns a probability of scoring to each location on the field, representing the team’s threat level.
The threat level can be used by the opponent to reason about the effect of possible defensive tactics, which is the focus of this paper. The authors demonstrate how one can reason about possible strategies for reducing the opponent’s scoring opportunities by analyzing the opponent’s MRP (i.e., MDP with a fixed policy) and forcing them to avoid certain critical locations on the field. Specifically, the authors look at the crucial locations for generating shots and buildup play, and assess how effective these defensive strategies remain after the offensive team adapts to them. This approach provides valuable insights into the decision-making process of soccer teams and can help coaches and analysts optimize their team’s performance by analyzing and adapting to different strategies.
Shot Suppression
The paper presents two approaches for suppressing shots in soccer games: indirect shot suppression and direct shot suppression. The yellow shaded region in Figure 2, which includes shot locations, accounts for approximately 91% of all shots taken during a game.
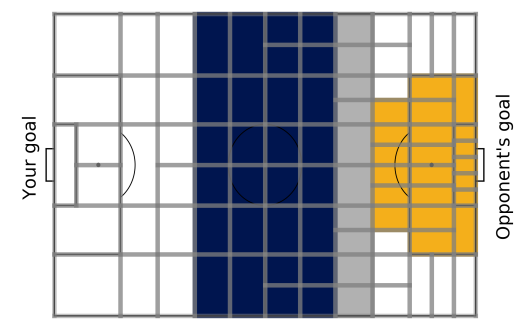
Indirect shot suppression aims to limit the number of times the opponent reaches this region, thereby indirectly suppressing shots. To determine how likely an opponent is to reach shot locations from a given location, the probability of reaching shot locations from a location f is computed using a query:
To assess the effect of a counterfactual policy where the opposing team avoids entering a specific location f0, the probability of reaching shot locations from f is computed using:
By computing the percentage decrease in the probability of reaching shot locations when forced to avoid f0 for all locations in non-shot, Formula 4 can be used to measure the importance of f0 for indirectly suppressing shots.
Manchester City’s and Burnley’s most important states for indirect shot suppression lie centrally, outside the shooting locations and on the right side of the penalty box, respectively. Preventing Manchester City’s and Burnley’s entry into their most important states decreases their chance of reaching the shooting locations by almost 20% and just over 9%, respectively.

Direct shot suppression aims to limit the number of shots an opponent takes, reducing the chances of conceding. To assess a team’s likelihood of generating shots, the probability of a sequence starting in location f and eventually resulting in a shot from shot locations is computed using:
The probability of shooting is computed using the below equation and is used to assess the effect of forcing the opposing team to avoid entering a specific location f0.
Formula 7 can then be used to measure each state’s importance for directly suppressing shots by computing the percentage decrease in the probability of shooting when forced to avoid f0 for all locations in non-shot. Manchester City’s and Burnley’s most important states for direct shot suppression lie centrally and on the right side of the penalty box, respectively. Preventing entry into these locations decreases Manchester City’s and Burnley’s chances of shooting by almost 10% and 4%, respectively.
Movement Suppression
In this section of the paper, the authors introduce a method for suppressing the movement of the opponent team in order to reduce their chance of scoring during the build-up phase of an attack. The method focuses on two regions of the field: the final third entry region and the middle third region. The authors define a set of states in these regions that an opposing team should prevent their opponent from entering to decrease their chance of scoring by a certain percentage. The authors use Equations 8 and 9 to formulate this query. Equation 8 computes the difference in the probability of scoring between a given state and a set of states that the opponent should avoid. Equation 9 finds a cluster of states around a given state where the probability of reaching that state from any of the other states in the cluster is greater than a threshold value.
The authors demonstrate the effectiveness of this method by applying it to Manchester City and Liverpool. By avoiding certain areas of the field, the authors were able to reduce the chance of scoring from each of the final third entry states by at least 10%. For Manchester City, the crucial areas to avoid were located around the center and left side of the field, where their creative players operate. For Liverpool, the crucial areas to avoid were a mirrored version of those of Manchester City, located on the middle and right side of the field, where their attacking wing-back and player of the season operate. The authors also show that decreasing the chance of scoring by at least 1% in each state in the middle third of the field can be achieved by forcing the opponent team to avoid the center of their defensive third.
Evaluating the Effect of Adapting the Policy
In this section, the authors explore the effect of a team adapting their old policy (π) towards a new policy (π0) in response to an opponent’s strategy of forcing them to avoid certain areas. The new policy (π0) simply stops trying to reach locations in the area, and the lost probability mass is redistributed over all other states. By fixing the new policy (π0) in the team’s MDP, the authors reason about the effect on the chances of scoring while adapting to being forced to avoid the area. This is quantified using Equation 11, where Vπ(f) and Vπ0(f) represent the expected value of state f under policies π and π0, respectively.
The authors illustrate the effect of Manchester City and Liverpool adapting their policies to an opponent’s strategy of forcing them to avoid certain areas. The results show that forcing Manchester City to avoid a certain area reduces their chance of scoring by 16.9%. However, when they adjust their policy, the decrease is reduced to 3.9%. Similarly, forcing Liverpool to avoid a certain area decreases their chance of scoring by 12.3%, and when they adjust their policy, the decrease is reduced to 4%. While the decrease is less impressive in the latter case for both teams, it still represents a reasonable reduction given that adapting one’s strategy is hard.

Related Work
This section of the paper discusses related work on using Markov models in sports and specifically in soccer. The authors note that Markov models are often used to quantify a player’s contributions during a match, but using these models for tactical advice has received less attention. Some approaches have used Markov reward processes (MRPs) to analyze set-pieces and determine the optimal times for substitutions and tactical changes, while others have used the optimal policy of an MDP to provide tactical advice. However, the authors’ proposed MDP differs from these approaches in that it takes a defensive perspective and uses probabilistic model checking to assess the effect of employing different defensive strategies.
The authors also discuss the use of MDPs in research on strategic reasoning and planning in simulated robot soccer, where Q-learning and automated action planning strategies have been developed for in-game decision making. However, the authors note that such approaches cannot immediately be used in real-life soccer due to the game’s high unpredictability. Instead, the authors aim to identify dangerous situations and evaluate the effects of specific forced changes to a team’s policy to inform tactical planning by coaches.
Finally, the authors note that applying verification techniques to sports models has not been extensively explored. While some previous work has applied probabilistic model checking to tennis and soccer models to predict win probability and identify the best action, the authors’ work is the first, to the best of their knowledge, to apply probabilistic model checking to inform a defensive game plan in soccer.
Conclusion
In this research paper, the authors have demonstrated the applicability of machine learning techniques to learn a model that can be used to reason about goal-directed policies in professional soccer, which can also be extended to other environments. They have proposed an approach that can be used to provide defensive tactical advice to soccer teams by applying probabilistic model checking to assess the effects of employing different defensive strategies. While there are no strong guarantees about the correctness of the model, the authors argue that it supports reasoning about strategies and policies with respect to safety (i.e., reducing the chance of conceding). The results of the queries can also help human soccer experts better understand the effects of potential strategies, contributing to trustworthy AI. The proposed approaches can serve as a basis for future tactical analysis in sports.
Resources
Van Roy, M., Yang, W. C., De Raedt, L., & Davis, J. (2021). Analyzing learned markov decision processes using model checking for providing tactical advice in professional soccer. In AI for Sports Analytics (AISA) Workshop at IJCAI 2021.